Dr Harswaroop Sharma Mathematics Class 11 Solutions Pdf

RD SHARMA Solutions for Class 11-science Maths Chapter 18 - Binomial Theorem

Chapter 18 - Binomial Theorem Exercise Ex. 18.1

Question 1(i)

Solution 1(i)

Question 1(ii)

Solution 1(ii)

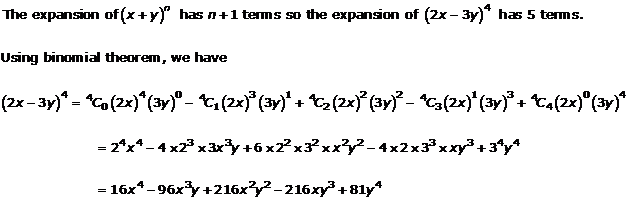
Question 1(iii)

Solution 1(iii)

Question 1(iv)

Solution 1(iv)

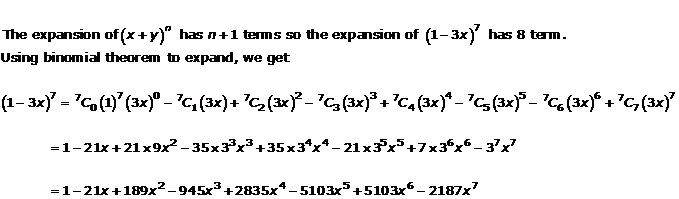
Question 1(v)

Solution 1(v)

Question 1(vi)

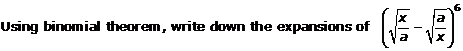
Solution 1(vi)

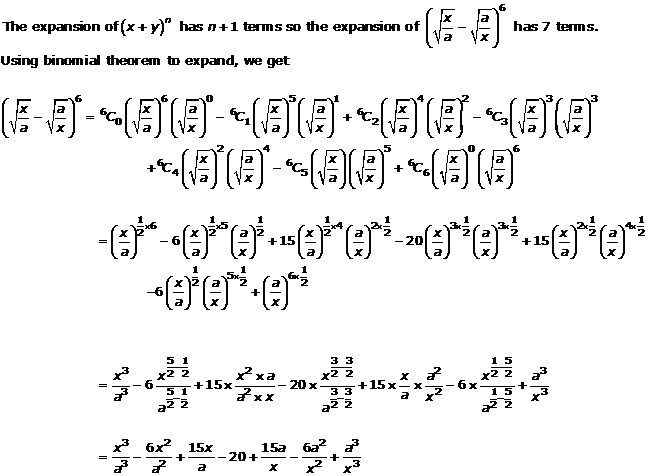
Question 1(vii)

Solution 1(vii)

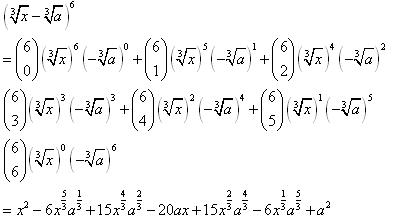
Question 1(viii)

Solution 1(viii)

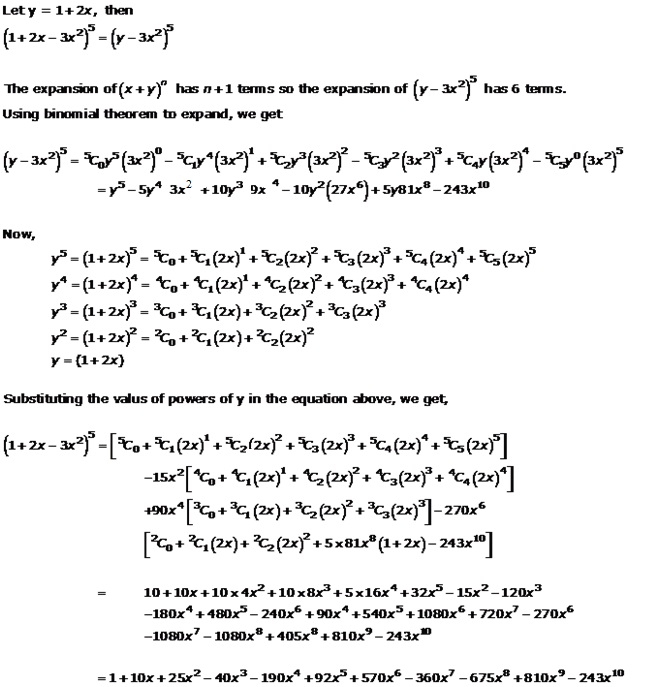
Question 1(ix)

Solution 1(ix)

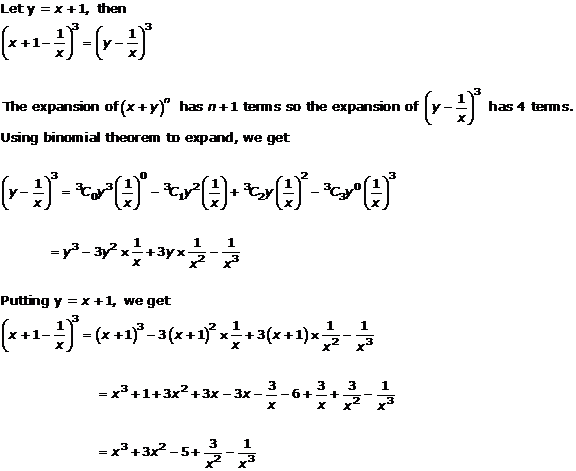
Question 1(x)

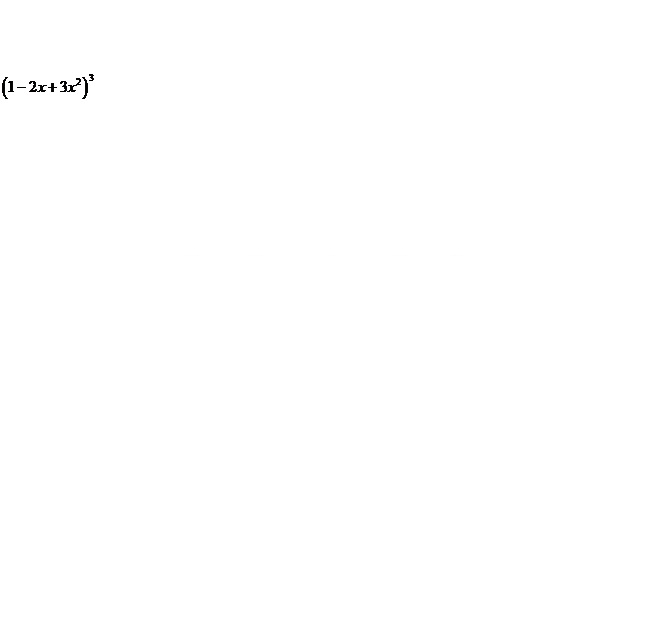
Solution 1(x)

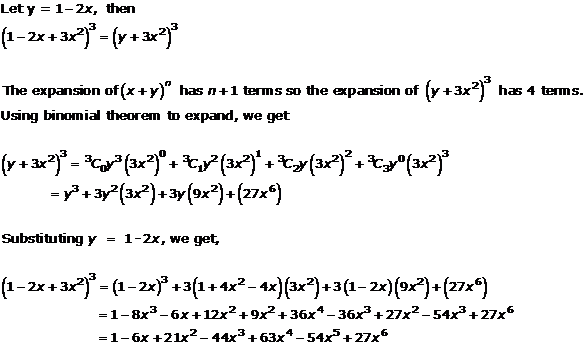
Question 2(i)

Solution 2(i)

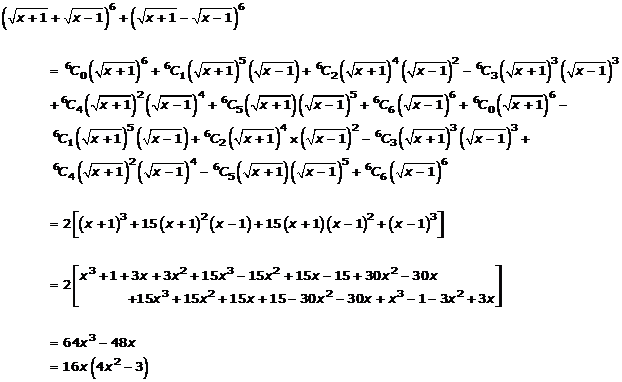
Question 2(ii)

Solution 2(ii)

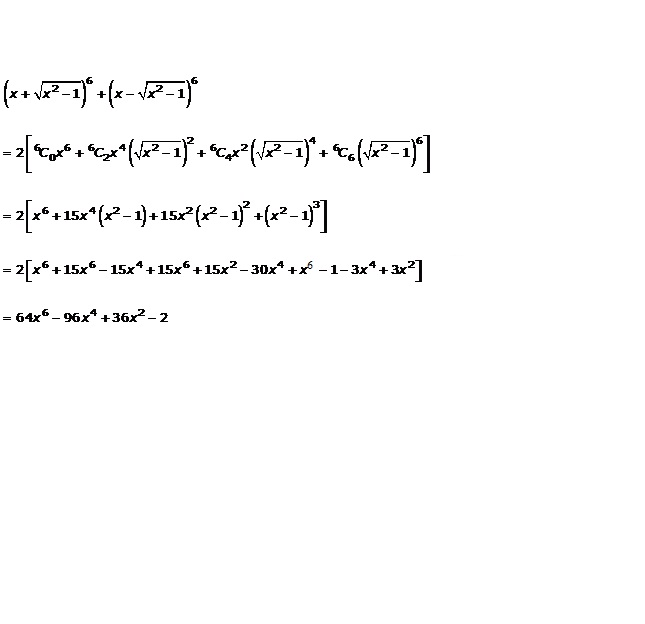
Question 2(iii)

Solution 2(iii)

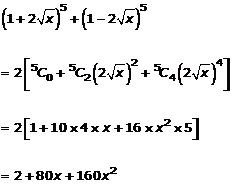
Question 2(iv)

Solution 2(iv)

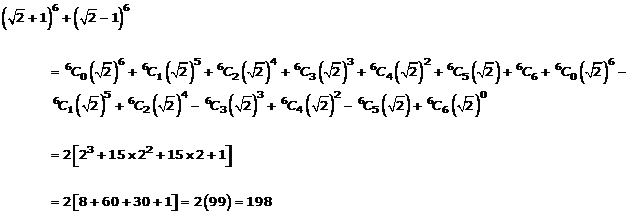
Question 2(v)

Solution 2(v)

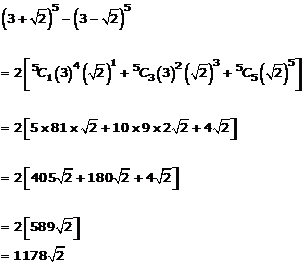
Question 2(vi)

Solution 2(vi)

Question 2(vii)

Solution 2(vii)

Question 2(viii)

Solution 2(viii)

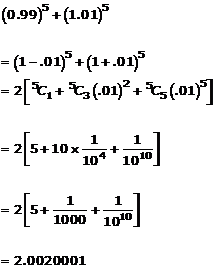
Question 2(ix)

Solution 2(ix)

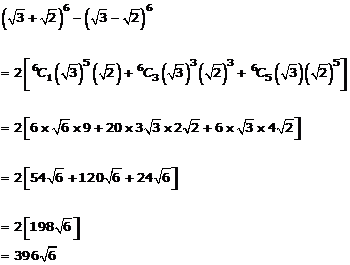
Question 2(x)

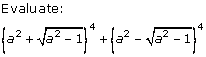
Solution 2(x)

Question 3

Solution 3

Question 4

Solution 4

Question 5(i)

Solution 5(i)

Question 5(ii)

Solution 5(ii)

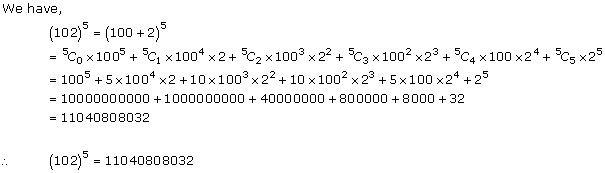
Question 5(iii)

Solution 5(iii)

Question 5(iv)

Solution 5(iv)

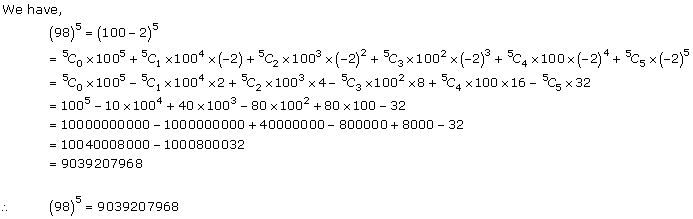
Question 6

Solution 6

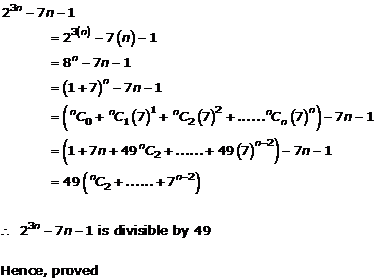
Question 7

Solution 7

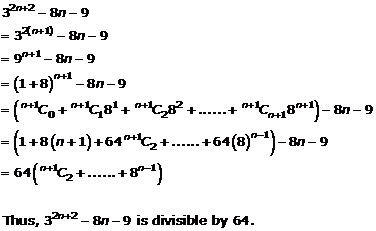
Question 8

Solution 8

Question 9

Solution 9

Question 10

Solution 10

Question 11

Solution 11

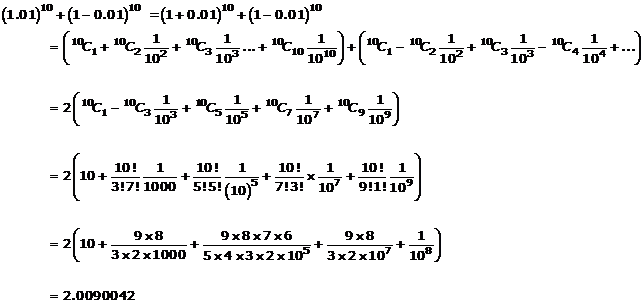
Question 12

Show that 2^{4n + 4} - 15n - 16, where n Î N is divisible by 225.

Solution 12

Chapter 18 - Binomial Theorem Exercise Ex. 18.2

Question 1

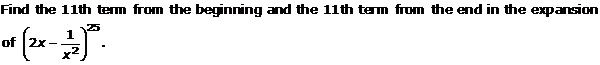
Solution 1

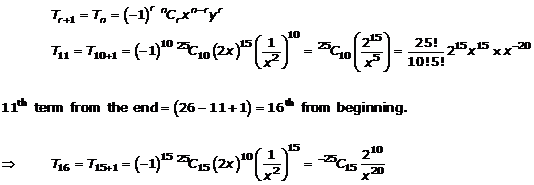
Question 2

Solution 2

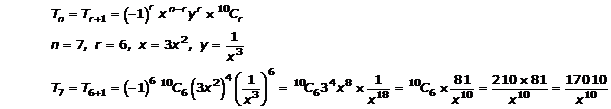
Question 3

Solution 3

Question 4

Solution 4

Question 5

Solution 5

Question 6

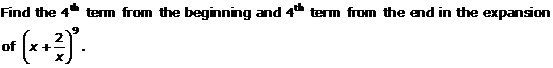
Solution 6

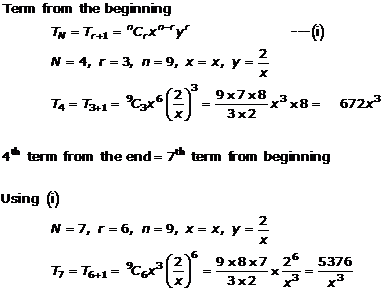
Question 7

Solution 7

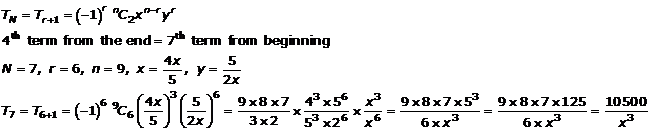
Question 8

Solution 8

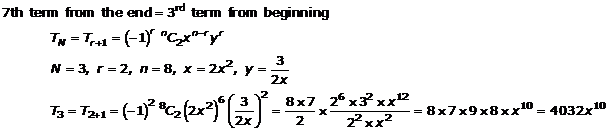
Question 9(i)

Solution 9(i)

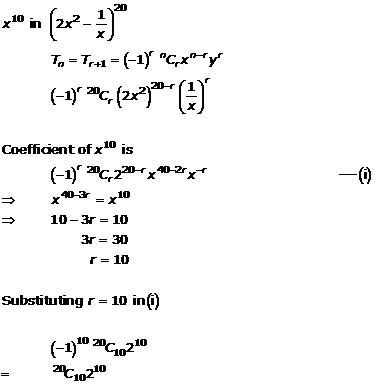
Question 9(ii)

Solution 9(ii)

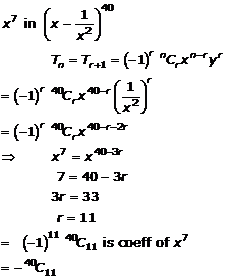
Question 9(iii)

Solution 9(iii)

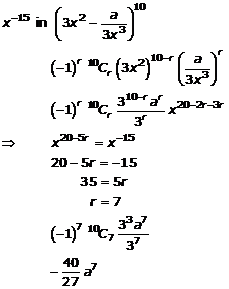
Question 9(iv)

Solution 9(iv)

Question 9(v)

Solution 9(v)

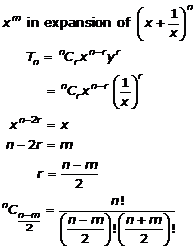
Question 9(vi)

Solution 9(vi)

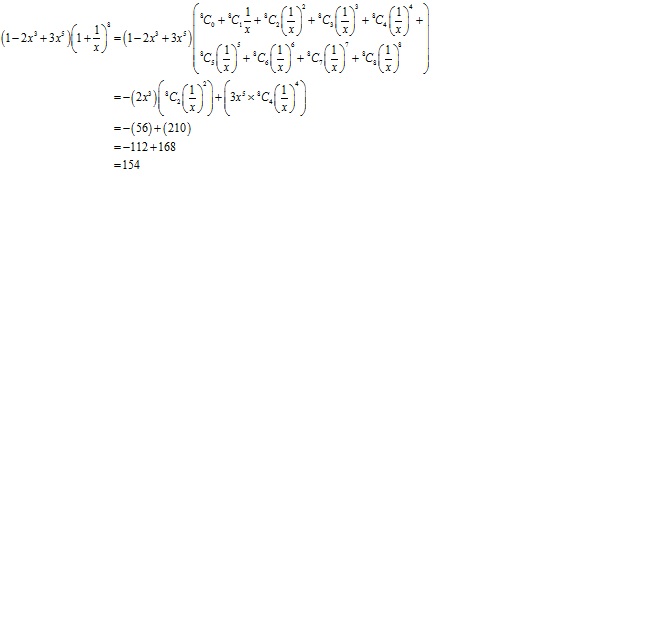
Question 9(vii)

Solution 9(vii)

Question 9(viii)

Find the coefficient of x in the expansion of

(1 - 3x + 7x²) (1 - x)¹⁶ .

Solution 9(viii)

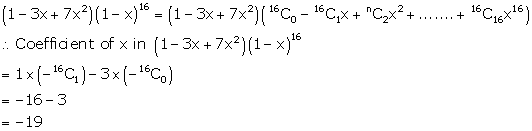
Question 10

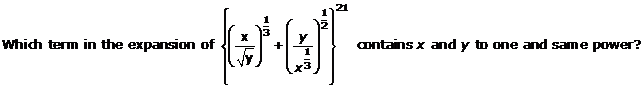
Solution 10

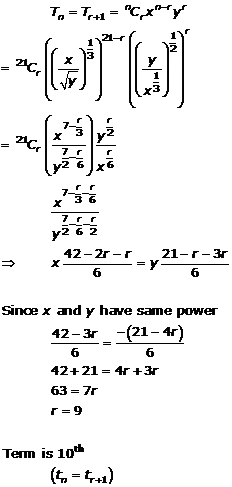
Question 11

Solution 11

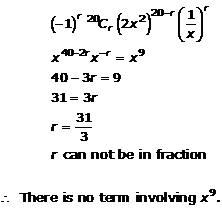
Question 12

Solution 12

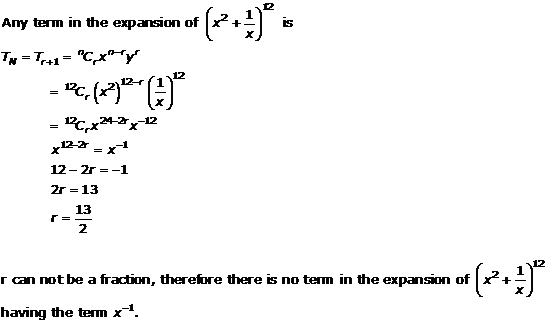
Question 13(i)

Solution 13(i)

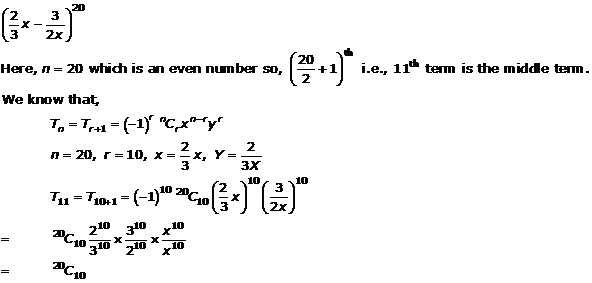
Question 13(ii)

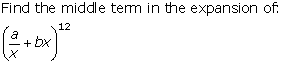
Solution 13(ii)

Question 13(iii)

Solution 13(iii)

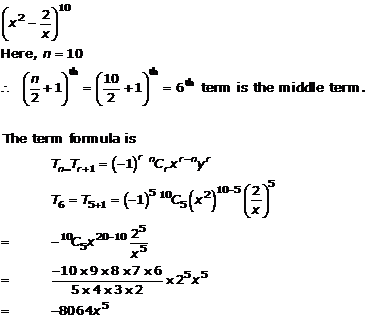
Question 13(iv)

Solution 13(iv)

Question 14(i)

Solution 14(i)

Question 14(ii)

Solution 14(ii)

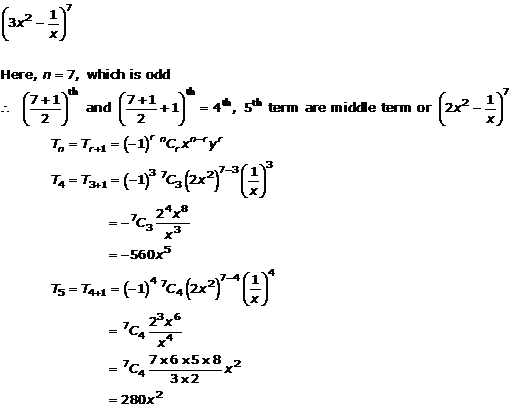
Question 14(iii)

Solution 14(iii)

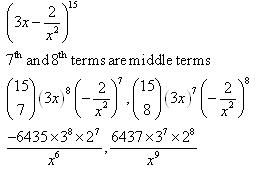
Question 14(iv)

Solution 14(iv)

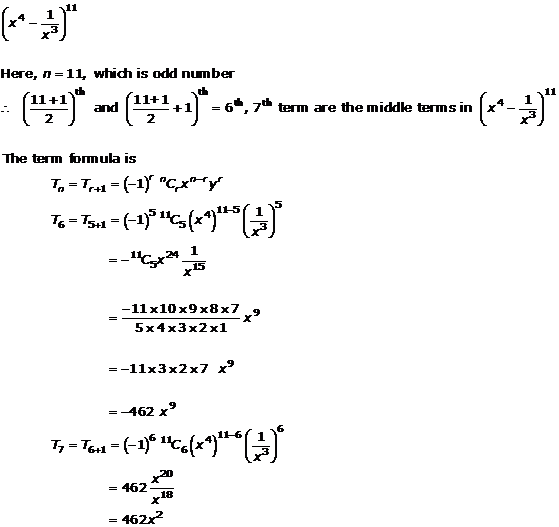
Question 15(i)

Solution 15(i)

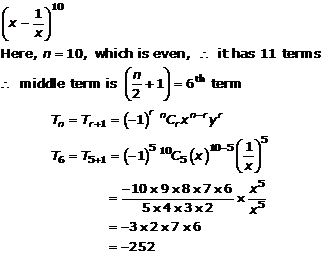
Question 15(ii)

Solution 15(ii)

Question 15(iii)

Solution 15(iii)

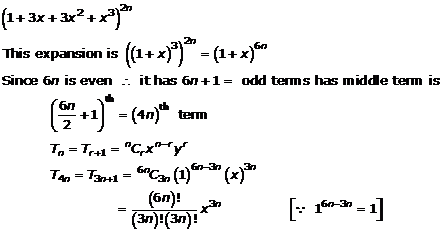
Question 15(iv)

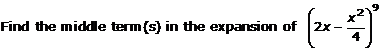
Solution 15(iv)

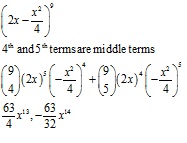
Question 15(v)

Solution 15(v)

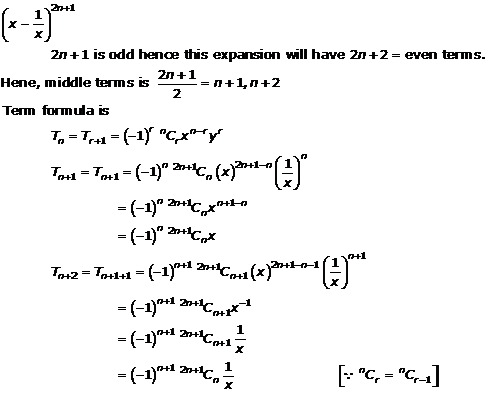
Question 15(vi)

Solution 15(vi)

Question 15(vii)

Solution 15(vii)

Question 15(viii)

Find the middle term (s) in expansion of:

Solution 15(viii)

Question 15(ix)

Find the middle term (s) in expansion of:

Solution 15(ix)

Question 15(x)

Find the middle term (s) in expansion of:

Solution 15(x)

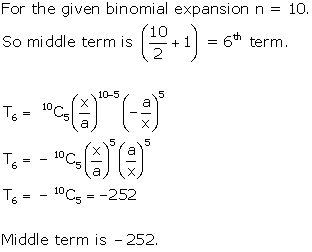
Question 16(i)

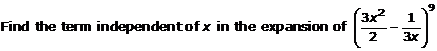
Solution 16(i)

Question 16(ii)

Solution 16(ii)

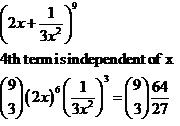
Question 16(iii)

Solution 16(iii)

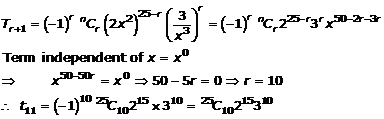
Question 16(iv)

Solution 16(iv)

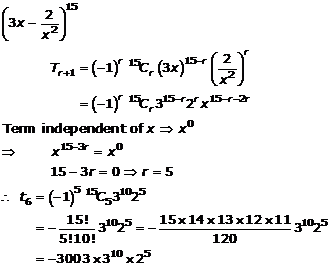
Question 16(v)

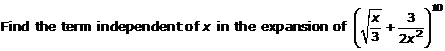
Solution 16(v)

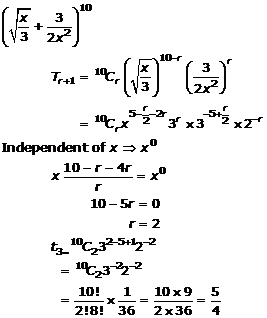
Question 16(vi)

Solution 16(vi)

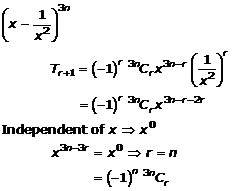
Question 16(vii)

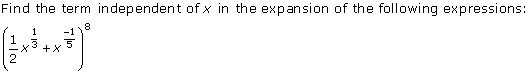
Solution 16(vii)

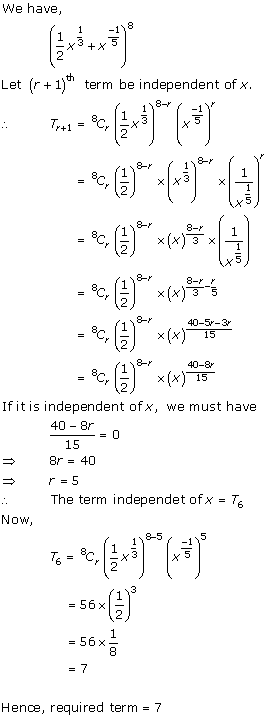
Question 16(viii)

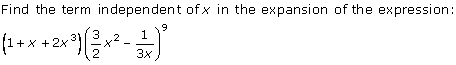
Solution 16(viii)

Question 16(ix)

Solution 16(ix)

Question 16(x)

Solution 16(x)

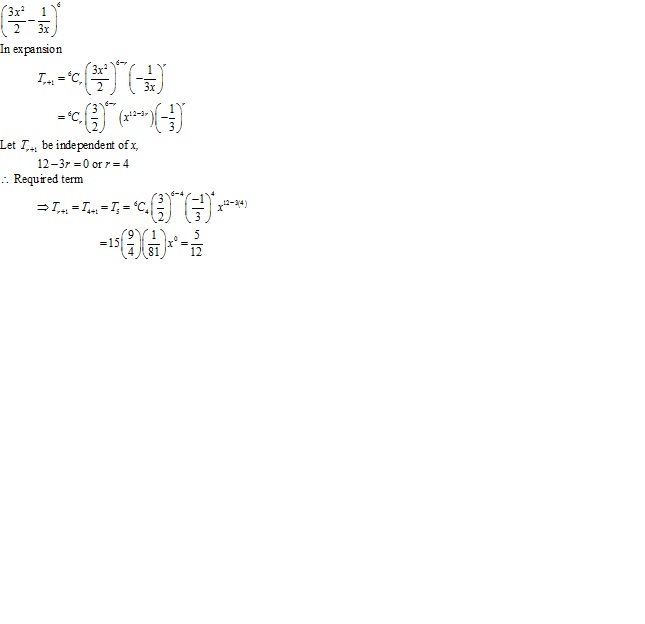
Question 17

Solution 17

Question 18

Solution 18

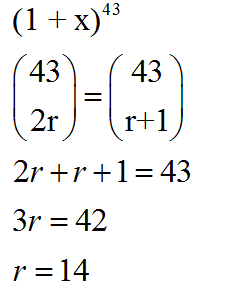
Question 19

Solution 19

Question 20

Solution 20

Question 21

Solution 21

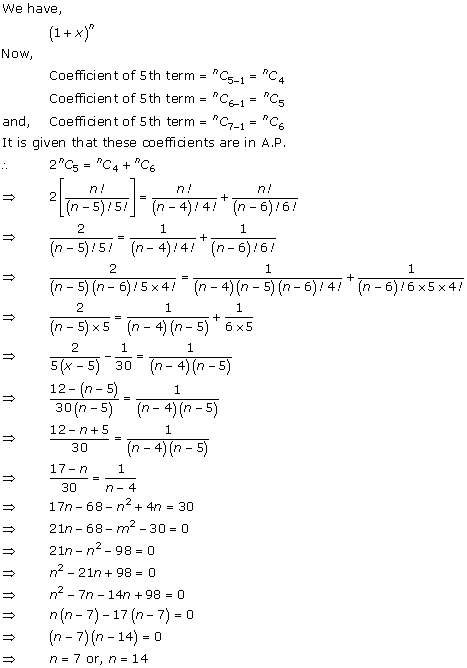
Question 22

Solution 22

Question 23

Solution 23

Question 24

Solution 24

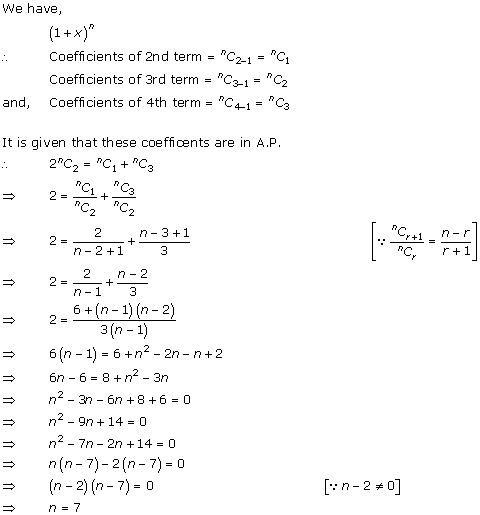
Question 25

Solution 25

Question 26

Solution 26

Question 27

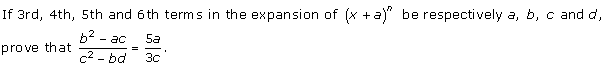
Solution 27

Question 28

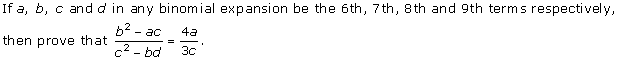
Solution 28

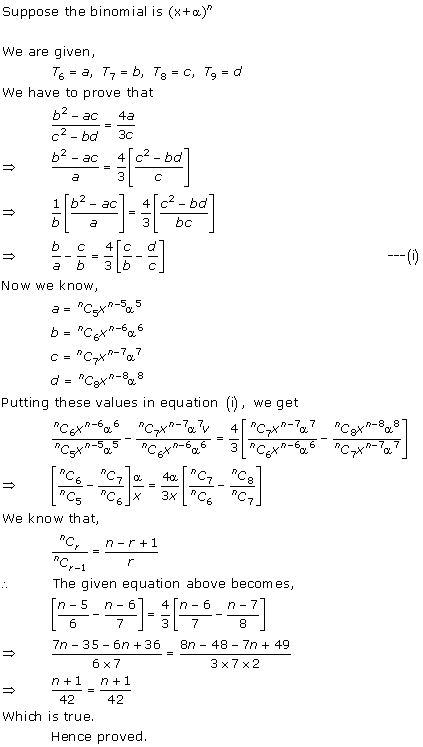
Question 29

Solution 29

Question 30

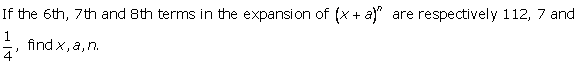
Solution 30

Question 31

Solution 31

Question 32

Solution 32

Question 33

Solution 33

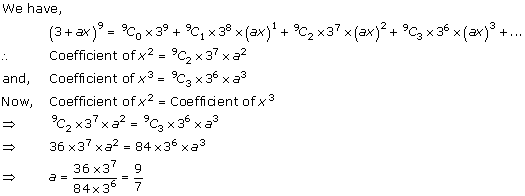
Question 34

Solution 34

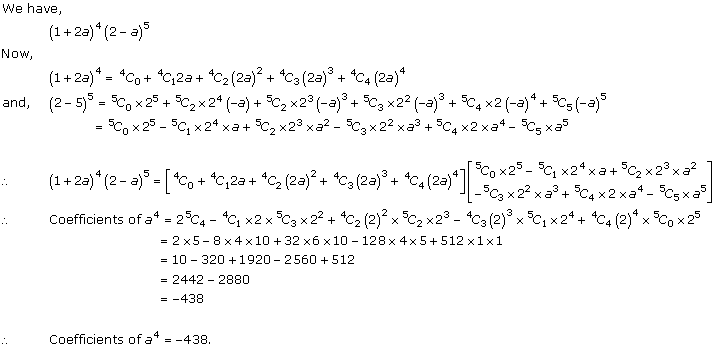
Question 35

Solution 35

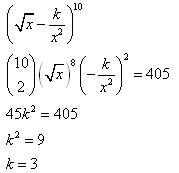
Question 36

Solution 36

Question 37

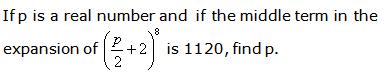
Solution 37

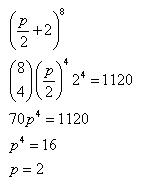
Question 38

Solution 38

Question 39

If the seventh term from the beginning and end in the binomial expansion of 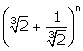are equal, find n.

Solution 39

Chapter 18 - Binomial Theorem Exercise Ex. 18VSAQ

Question 1

Write the number of terms in the expansion of .

Solution 1

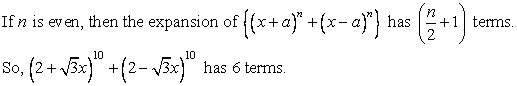
Question 2

Write the sum of coefficients in the expansion of (1 - 3x + x²)¹¹¹.

Solution 2

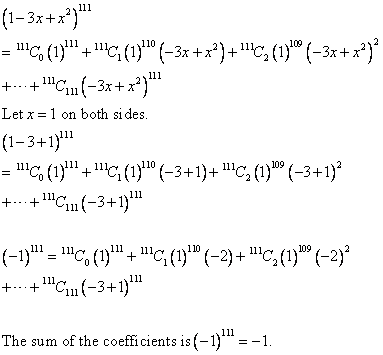
Question 3

Write the number of terms in the expansion of

(1 - 3x + 3x² - x³)⁸.

Solution 3

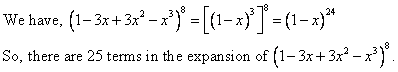
Question 4

Write the middle term in the expansion of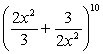

Solution 4

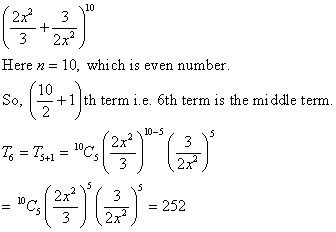
Question 5

Which term is independent of x, in the expansion of

Solution 5

Question 6

If a and b denote respectively the coefficient of x^m and xⁿ in the expansion of (1 + x) ^m+n , then write the relation between a and b.

Solution 6

Question 7

IF a and b are coefficients of xⁿ in the expansion of (1 + x)²ⁿ and (1 + x)^2n-1 respectively, then write the relation between a and b.

Solution 7

Question 8

Write the middle term in the expansion of

Solution 8

Question 9

If a and b denote the sum of the coefficients in the expansion of (1 - 3x + 10x²)ⁿ and (1 + x²)ⁿ respectively, then write the relation between a and b.

Solution 9

Question 10

Write the coefficient of the middle term in the expansion of (1 + x)²ⁿ .

Solution 10

• My Class
• Videos
• Undoubt
• Test
• Plans
• My Profile

Dr Harswaroop Sharma Mathematics Class 11 Solutions Pdf

Source: https://www.topperlearning.com/rd-sharma-solutions/cbse-class-11-science-mathematics/r-d-sharma-mathematics/binomial-theorem

Posted by: dumaisention.blogspot.com

Share this post